Помехоустойчивое кодирование: Голографический код для надежной связи
Что такое помехоустойчивое голографическое кодирование
Помехоустойчивое голографическое кодирование — это хитрый метод защиты данных, который берет на вооружение принципы оптической голографии. Его фишка в том, что он позволяет восстановить изначальное сообщение, даже если канал связи сильно шумит и вносит искажения. Главный козырь здесь — свойство делимости голограммы. За счет этой делимости мы получаем избыточность, которая помогает "вытащить" данные, даже если ошибок накопилось много.
Этот подход переносит оптические фокусы по восстановлению волнового фронта прямо в кодирование обычных цифровых данных. В отличие от обработки картинок, где небольшая неточность — это не конец света, здесь нам нужна абсолютная точность: декодированный блок должен в точности совпадать с оригиналом.
Чтобы не увязнуть в расчетах, данные представляют в виде единичного позиционного кода. По сути, информация кодируется положением одной-единственной активной точки. Из этого рождается самая простая голограмма — зонная пластинка Френеля.
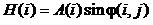
Как работает голографическое кодирование
Голографический метод моделирует одномерную голограмму, которую создает волна от входного блока. Его отличие от "настоящей" оптики в том, что объект здесь одномерный и не зависит от реальных пространственных измерений.
Алгоритм кодирования: от данных к голограмме
Процесс кодирования — это превращение двоичного кода в некий пространственный объект и последующий расчет интерференционной картины.
1. Преобразование данных: Мы берем $k$-разрядный двоичный код $X$ и превращаем его в блок $A$ длиной $n=2k$ точек. В этом блоке будет только одна единица — ровно там, где у нас было значение $X$. Остальные точки — нули. Так мы создаем избыточность $r = n - k$ и получаем скорость кода $R = k/n$.
2. Моделирование объекта: Блок $A$ мы представляем как светящуюся точку на абсолютно черном фоне.
3. Формирование голограммы: Теперь рассчитываем зонную линейку Френеля $H(j)$, основываясь на фазе сферической волны, которая исходит от этой активной точки объекта.
$$H(j) = \sum_{i=1}^{n} \cos \left( \frac{2\pi}{\lambda} \left( L + \sqrt{L^2 + (i-j)^2 d^2} \right) \right) \pmod{1}$$
Здесь $\lambda = d$.
4. Бинаризация: Полученную голограмму $H(j)$ округляем до одного бита, получая кодовое слово $HO(j)$. Вся информация о $X$ "зашита" в номере позиции этой зонной линейки.
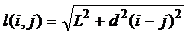
Алгоритм декодирования: восстановление информации
Декодирование стартует, когда мы приняли искаженный массив $HR(j)$. Каждая точка этого принятого массива рассматривается как источник своей сферической волны.
1. Восстановление объекта: Мы вычисляем восстановленный объект $AR(i)$ путем интерференции волн от всех принятых точек:
$$AR(i) = \sum_{j=1}^{n} \cos \left( \frac{2\pi}{\lambda} \left( L + \sqrt{L^2 + (i-j)^2 d^2} \right) \right)$$
2. Поиск максимума: Находим позицию $Y$, где массив $AR(i)$ достигает своего пика. Это значение $Y$ и становится нашим выходным блоком данных $X_R$.
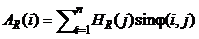
Если в канале был шум, то нам придется смотреть на отношение амплитуды пика к уровню шума. Это отношение напрямую влияет на то, насколько вероятно, что результат будет верным.
Сравнение эффективности с другими кодами
Мы протестировали эффективность голографического кода, смоделировав работу в MATLAB на канале с аддитивным белым гауссовским шумом (AWGN).
Устойчивость к случайным ошибкам
Этот код показывает себя очень крепким бойцом. Возьмем, к примеру, длину кодовой комбинации $n=256$ и $k=8$. Код спокойно переживает 80 случайных ошибок (это целых 31% длины слова!), а вероятность ошибки декодирования при этом минимальна — всего $0.00005$ (после 100 000 тестов).
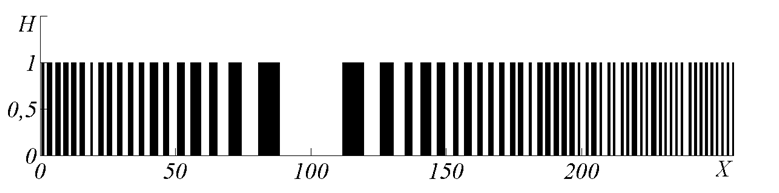
- Рис. 1. Одномерная голограмма (последовательность нулей и единиц) в кодовом слове диной n=256*
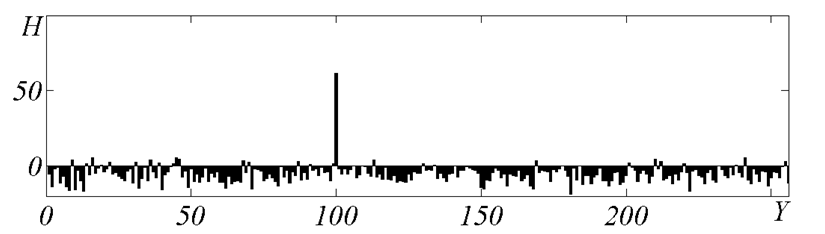
- Рис. 2. Результат декодирования при n=256, уровень шума S/N=0 дБ, декодированное значение Y=100*
Преимущества перед РС- и РМ-кодами
Даже при скорости $R=1/32$ голографический код вырывается вперед.
- РС-код (Рида-Соломона), имея ту же избыточность, может исправить лишь около 6% случайных ошибок.
- Голографический код дает нам выигрыш 2 дБ по сравнению с мажоритарным кодом, когда нам нужна вероятность ошибки $10^{-6}$ (при $S/N = -7$ дБ).
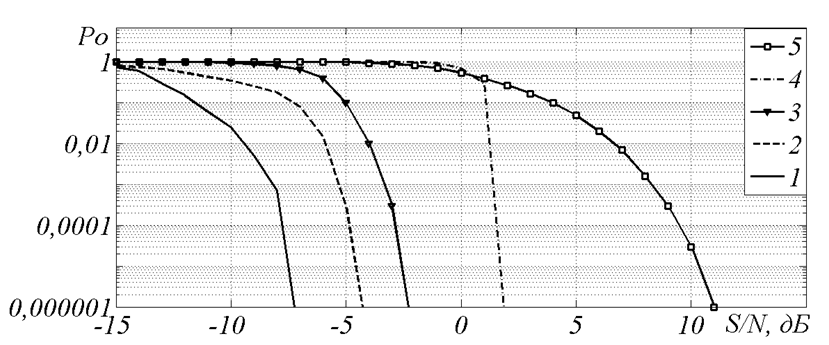
- Рис. 4. Зависимость вероятности ошибки декодирования Po от отношения сигнал/шум при скорости кода R=1/32.*
Коррекция пакетных ошибок
В мобильной связи частенько случаются пакетные ошибки (замирания). Здесь классические коды попадают в ловушку: им нужно выбирать между прямым и инвертированным результатом.
А вот голографический код эту проблему решает элегантно. Максимум восстанавливается одинаково хорошо, неважно, положительное изображение мы получили или инвертированное. При 100% пакетных ошибок (когда всё слово перевернулось) декодирование проходит без сучка и задоринки.
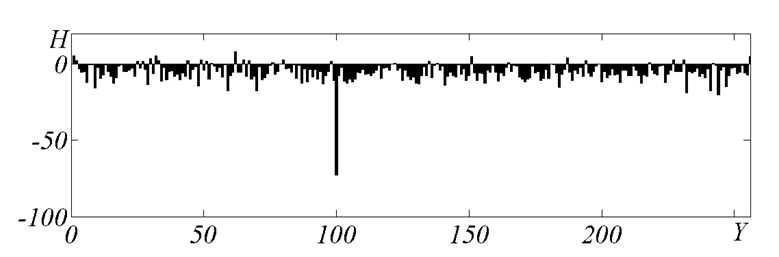
- Рис. 6. Результат декодирования при 100% пакетных ошибок*
Более того, этот код способен исправить до 100% пакетных ошибок! Как? Используя метод разбиения на четверти и обработки в инвертированном виде. Это круче, чем предел в 50%, который наблюдается у РС-кодов.
Снижение вычислительной сложности
С точки зрения алгоритмов, декодирование голографического кода проще, чем у его традиционных конкурентов.
Для декодирования РС-кодов часто приходится решать громоздкие системы линейных уравнений (тот же метод Гаусса), а сложность растет как $t^3$, где $t$ — количество исправляемых ошибок.
Декодирование голографического кода требует $n^2$-кратного вычисления $AR(i)$ по формуле (2). Звучит не очень, да? Но честно говоря, алгоритмическая сложность здесь ниже, и сами вычисления куда менее прожорливы, чем алгебраические методы.
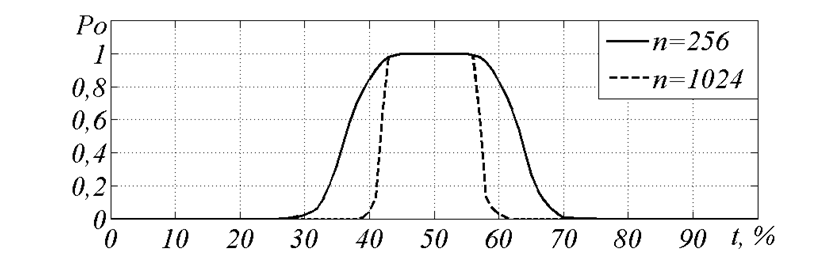
- Рис. 7. Зависимость вероятности ошибки декодирования PO от числа ошибок t при длинах кода n=256 и n=1024*
Финал
- *Голографический код — это просто зверь в плане помехоустойчивости. Он способен "проглотить" до 40% случайных независимых ошибок и выдержать 100% пакетных ошибок**. Это очень перспективное решение для каналов с плохим соотношением сигнал/шум, скажем, в космической или мобильной связи. 🚀
Если тебе нужна железобетонная надежность передачи данных в самых суровых условиях, присмотрись к этому методу. Подумай о внедрении помехоустойчивого голографического кодирования в свои системы!