Что такое FizzBuzz и как его усложнить
FizzBuzz — это простая игра для проверки базовых навыков программирования, где числа заменяются словами "Fizz" (на 3), "Buzz" (на 5) или "FizzBuzz" (на 15). Классическое решение использует условные операторы (if/elif/else). Однако, можно усложнить эту задачу, представив правила игры в виде аналитического выражения с использованием тригонометрических функций, например, косинусов.
Эта статья покажет, как математически закодировать логику FizzBuzz в единую формулу, избегая привычных условных конструкций. Мы преобразуем игру в дискретный ряд Фурье.
Как определить последовательность FizzBuzz математически
Чтобы создать аналитическое выражение, сначала нужно формализовать правила игры. Последовательность FizzBuzz основана на делимости числа n на 3 и 5.
Мы вводим набор символьных функций, которые генерируют элементы игры. Для любого целого числа n определим четыре функции:
f(n) = n(возвращает само число).F(n),B(n),FB(n)— константные функции, возвращающие "Fizz", "Buzz", "FizzBuzz" соответственно.
Последовательность FizzBuzz $S(n)$ определяется выбором одной из этих функций в зависимости от делимости $n$:
$$S(n) = \begin{cases} \text{FizzBuzz}, & \text{если } 3|n \text{ и } 5|n \\ \text{Fizz}, & \text{если } 3|n \text{ и } 5 \nmid n \\ \text{Buzz}, & \text{если } 3 \nmid n \text{ и } 5|n \\ n, & \text{в противном случае} \end{cases}$$
Где $a|b$ означает, что $a$ делит $b$.
Первые члены последовательности $S(n)$ для $n=1, 2, \dots, 15$:
Функция $I(n)$ называется индексной, так как она выбирает нужный символ на основе $n$.
Зачем нужны индикаторные функции для FizzBuzz
Индексная функция $I(n)$ кусочная. Наша цель — заменить её единым выражением. Для этого вводятся индикаторные функции, которые помогают преобразовать условия делимости в числовой вид.
Индикаторная функция $\chi_k(n)$ возвращает 1, если $k$ делит $n$, и 0 в противном случае.
$$\chi_k(n) = \begin{cases} 1, & \text{если } k|n \\ 0, & \text{если } k \nmid n \end{cases}$$
Используя эти функции, можно переписать индекс $I(n)$:
Таблица сопоставления двоичных значений, полученных через индикаторные функции, и десятичных чисел:
Например, для $n=6$ (или $110_2$), $\chi_3(6)=1$ и $\chi_5(6)=0$. Это соответствует двоичной записи $10$, что равно числу 2. Таким образом, $\chi_3(n)$ и $\chi_5(n)$ дают двоичное представление индекса.
Это упрощает поиск паттернов, но мы всё ещё используем условную логику.
Преобразование в формулу с косинусами
Что делать, если использование индикаторных функций запрещено, и мы должны использовать только стандартные операции, включая тригонометрические? Мы можем выразить делимость через косинус.
Ключевым моментом является формула, связывающая делимость с косинусами через формулу Эйлера ($e^{ix} = \cos(x) + i \sin(x)$).
Для любого целого $m$, мы имеем:
$$\cos\left(\frac{2\pi m}{3}\right) = \begin{cases} 1, & \text{если } 3|m \\ -1/2, & \text{если } 3 \nmid m \end{cases}$$
Это позволяет создать тригонометрические аналоги для проверки делимости на 3 и 5.
Например, функция, возвращающая 1, если $n$ кратно 3, и 0 в противном случае, может быть выражена через косинус:
$$\frac{1}{2}\left(1 + \cos\left(\frac{2\pi n}{3}\right)\right) = \begin{cases} 1, & \text{если } 3|n \\ 0, & \text{если } 3 \nmid n \end{cases}$$
Используя эти преобразования, можно получить аналитическое выражение для индексной функции $I(n)$ через косинусы:
$$I(n) = 1 + \left[1 - \cos\left(\frac{2\pi n}{3}\right)\right] + \frac{1}{2}\left[1 - \cos\left(\frac{2\pi n}{5}\right)\right] + \frac{1}{4}\left[1 - \cos\left(\frac{2\pi n}{15}\right)\right]$$
Это выражение, которое можно упростить до:
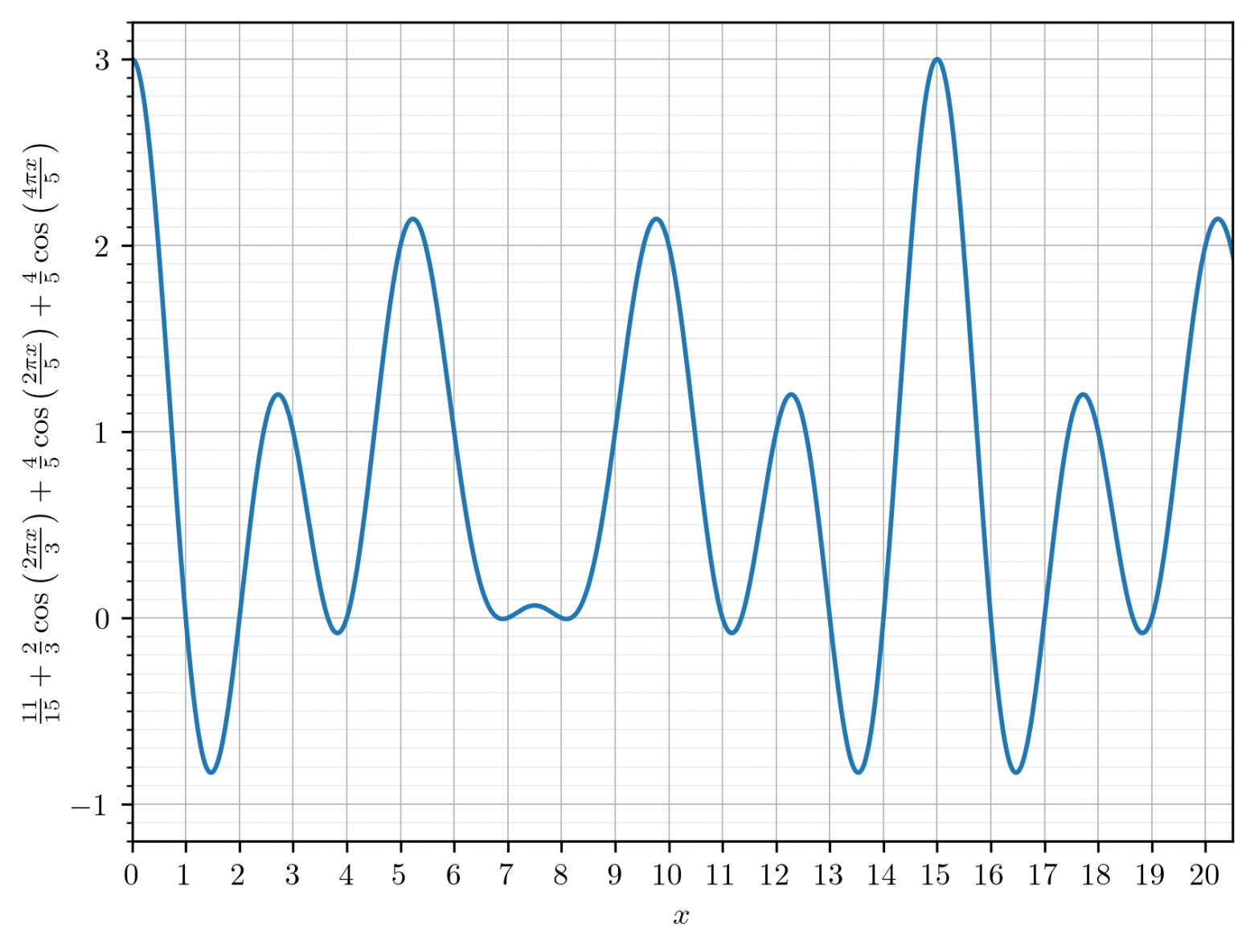
Давайте посмотрим на графическое представление этой функции в целочисленных точках:
График 
В целочисленных точках эта функция принимает нужные нам значения: $0, 1, 2, 3$.
Реализация FizzBuzz с использованием косинусов на Python
Мы можем использовать полученное выражение для генерации последовательности, заменяя условные операторы математическими вычислениями.
import math
def fizzbuzz_cosine(n):
# Вычисление индекса I(n) с помощью тригонометрической формулы
# Коэффициенты взяты из аналитического вывода
coeff_3 = 1.0 - math.cos(2 * math.pi * n / 3)
coeff_5 = 1.0 - math.cos(2 * math.pi * n / 5)
coeff_15 = 1.0 - math.cos(2 * math.pi * n / 15)
# Упрощенная формула (IMAGE_113)
index = 1 + coeff_3 + 0.5 * coeff_5 + 0.25 * coeff_15
# Округление до ближайшего целого, так как результат может быть
# очень близок к целому из-за погрешности float
idx = int(round(index))
results = {
0: str(n),
1: "Fizz",
2: "Buzz",
3: "FizzBuzz"
}
return results.get(idx, str(n))
# Пример вывода
for i in range(1, 16):
print(fizzbuzz_cosine(i))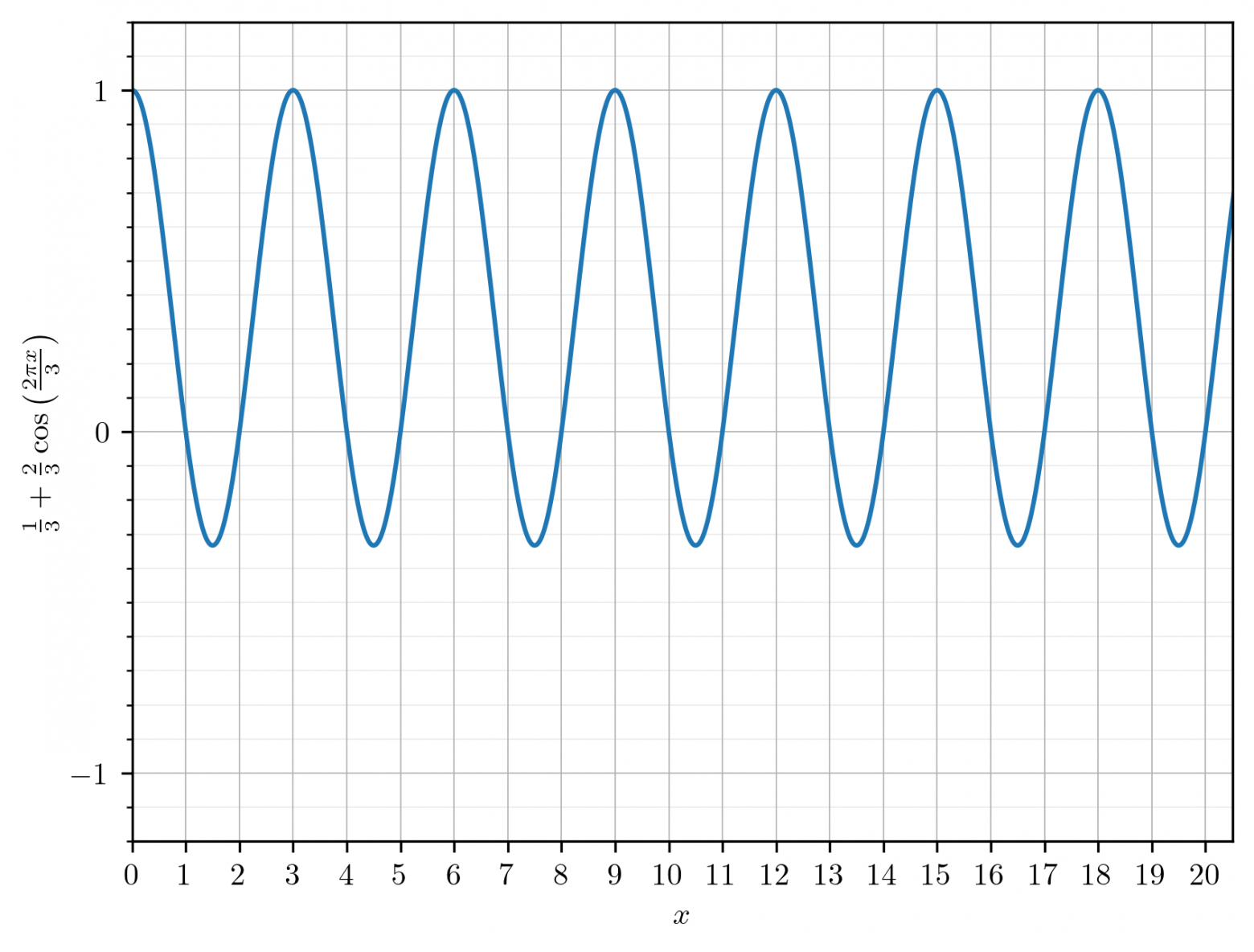
(График 
и другие графики показывают, как функция ведет себя в целом).
Дискретное преобразование Фурье для FizzBuzz
Полученное выражение для $I(n)$ — это, по сути, дискретный ряд Фурье. Он точно описывает любую периодическую функцию на конечной циклической группе.
Поскольку FizzBuzz имеет период 15 (повторяется каждые 15 чисел), мы можем получить то же самое выражение, применив дискретное преобразование Фурье (DFT) к набору значений $S(1)$ до $S(15)$.
DFT используется для нахождения коэффициентов ряда, а обратное DFT (IDFT) позволяет восстановить исходную функцию (нашу индексную функцию $I(n)$).
$$S(n) = \sum_{k=0}^{14} c_k e^{i 2\pi k n / 15}$$
Где $c_k$ — коэффициенты Фурье, вычисляемые через DFT.
Хотя ручное вычисление коэффициентов утомительно, современные инструменты (например, NumPy в Python) делают это мгновенно. Результат IDFT будет идентичен формуле, полученной с помощью косинусов.
Заключение
Мы успешно усложнили задачу FizzBuzz, представив её не через стандартные if/else, а через аналитическое выражение на основе дискретного ряда Фурье и косинусов.
Конечная формула для определения индекса $I(n)$ выглядит так:
$$I(n) = 1 + \left[1 - \cos\left(\frac{2\pi n}{3}\right)\right] + \frac{1}{2}\left[1 - \cos\left(\frac{2\pi n}{5}\right)\right] + \frac{1}{4}\left[1 - \cos\left(\frac{2\pi n}{15}\right)\right]$$
В Python это можно реализовать компактно:
print('\n'.join([fizzbuzz_cosine(i) for i in range(1, 16)]))Эта трансформация демонстрирует, как сложная логика может быть сведена к элегантному математическому виду, даже если это не всегда упрощает код.
- *Хотите применить сложные математические методы в ваших проектах? Свяжитесь с нами для консультации по анализу данных и оптимизации алгоритмов!**